The second law of thermodynamics is an expression of the tendency that over time, differences in temperature, pressure, and chemical potential equilibrate in an isolated physical system. From the state of thermodynamic equilibrium, the law deduced the principle of the increase of entropy and explains the phenomenon of irreversibility in nature. The second law declares the impossibility of machines that generate usable energy from the abundant internal energy of nature by processes called perpetual motion of the second kind.
The second law may be expressed in many specific ways, but the first formulation is credited to the German scientist Rudolf Clausius. The law is usually stated in physical terms of impossible processes. In classical thermodynamics, the second law is a basic postulate applicable to any system involving measurable heat transfer, while in statistical thermodynamics, the second law is a consequence of unitarity in quantum theory. In classical thermodynamics, the second law defines the concept of thermodynamic entropy, while in statistical mechanics entropy is defined from information theory, known as the Shannon entropy.
However, the concept of energy in the first law does not account for the observation that natural processes have a preferred direction of progress. For example, spontaneously, heat always flows to regions of lower temperature, never to regions of higher temperature without external work being performed on the system. The first law is completely symmetrical with respect to the initial and final states of an evolving system. The key concept for the explanation of this phenomenon through the second law of thermodynamics is the definition of a new physical property, the entropy.
A change in the entropy (S) of a system is the infinitesimal transfer of heat (Q) to a closed system driving a reversible process, divided by the equilibrium temperature (T) of the system.[1]
Empirical temperature and its scale is usually defined on the principles of thermodynamics equilibrium by the zeroth law of thermodynamics.[2] However, based on the entropy, the second law permits a definition of the absolute, thermodynamic temperature, which has its null point at absolute zero.[3]
The second law of thermodynamics may be expressed in many specific ways,[4] the most prominent classical statements[3] being the original statement by Rudolph Clausius (1850), the formulation by Lord Kelvin (1851), and the definition in axiomatic thermodynamics by Constantin Carathéodory (1909). These statement cast the law in general physical terms citing the impossibility of certain processes. They have been shown to be equivalent.
Note that it is possible to convert heat completely into work, such as the isothermal expansion of ideal gas. However, such a process has an additional result. In the case of the isothermal expansion, the volume of the gas increases and never goes back without outside interference.
 from the cooler reservoir to the hotter one, which violates the Clausius statement. Thus the Clausius statement implies the Kelvin statement. We can prove in a similar manner that the Kelvin statement implies the Clausius statement, or, in a word, the two are equivalent.
from the cooler reservoir to the hotter one, which violates the Clausius statement. Thus the Clausius statement implies the Kelvin statement. We can prove in a similar manner that the Kelvin statement implies the Clausius statement, or, in a word, the two are equivalent.
Carnot's theorem states that all reversible engines operating between the same heat reservoirs are equally efficient. Thus, any reversible heat engine operating between temperatures T1 and T2 must have the same efficiency, that is to say, the effiency is the function of temperatures only: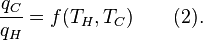
In addition, a reversible heat engine operating between temperatures T1 and T3 must have the same efficiency as one consisting of two cycles, one between T1 and another (intermediate) temperature T2, and the second between T2 andT3. This can only be the case if
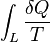 is path independent.
is path independent.
So we can define a state function S called entropy, which satisfies
For any irreversible process, since entropy is a state function, we can always connect the initial and terminal status with an imaginary reversible process and integrating on that path to calculate the difference in entropy.
Now reverse the reversible process and combine it with the said irreversible process. Applying Clausius inequality on this loop,
Notice that if the process is an adiabatic process,then δQ = 0, so .
.
Whatever changes to dS and dSR occur in the entropies of the sub-system and the surroundings individually, according to the Second Law the entropy Stot of the isolated total system must not decrease:
Now the heat leaving the reservoir and entering the sub-system is
It therefore follows that any net work δw done by the sub-system must obey
In sum, if a proper infinite-reservoir-like reference state is chosen as the system surroundings in the real world, then the Second Law predicts a decrease in X for an irreversible process and no change for a reversible process.
This approach to the Second Law is widely utilized in engineering practice, environmental accounting, systems ecology, and other disciplines.
Recognizing the significance of James Prescott Joule's work on the conservation of energy, Rudolf Clausius was the first to formulate the second law during 1850, in this form: heat does not flow spontaneously from cold to hot bodies. While common knowledge now, this was contrary to the caloric theory of heat popular at the time, which considered heat as a fluid. From there he was able to infer the principle of Sadi Carnot and the definition of entropy (1865).
Established during the 19th century, the Kelvin-Planck statement of the Second Law says, "It is impossible for any device that operates on a cycle to receive heat from a single reservoir and produce a net amount of work." This was shown to be equivalent to the statement of Clausius.
The ergodic hypothesis is also important for the Boltzmann approach. It says that, over long periods of time, the time spent in some region of the phase space of microstates with the same energy is proportional to the volume of this region, i.e. that all accessible microstates are equally probable over a long period of time. Equivalently, it says that time average and average over the statistical ensemble are the same.
It has been shown that not only classical systems but also quantum mechanical ones tend to maximize their entropy over time. Thus the second law follows, given initial conditions with low entropy. More precisely, it has been shown that the local von Neumann entropy is at its maximum value with a very high probability.[9] The result is valid for a large class of isolated quantum systems (e.g. a gas in a container). While the full system is pure and therefore does not have any entropy, the entanglement between gas and container gives rise to an increase of the local entropy of the gas. This result is one of the most important achievements of quantum thermodynamics[dubious ].
Today, much effort in the field is attempting to understand why the initial conditions early in the universe were those of low entropy[10][11], as this is seen as the origin of the second law (see below).
In terms of time variation, the mathematical statement of the second law for an isolated system undergoing an arbitrary transformation is:
 is the number of quantum states in a small interval between E and E + δE. Here δE is a macroscopically small energy interval that is kept fixed. Strictly speaking this means that the entropy depends on the choice of δE. However, in the thermodynamic limit (i.e. in the limit of infinitely large system size), the specific entropy (entropy per unit volume or per unit mass) does not depend on δE.
is the number of quantum states in a small interval between E and E + δE. Here δE is a macroscopically small energy interval that is kept fixed. Strictly speaking this means that the entropy depends on the choice of δE. However, in the thermodynamic limit (i.e. in the limit of infinitely large system size), the specific entropy (entropy per unit volume or per unit mass) does not depend on δE.
Suppose we have an isolated system whose macroscopic state is specified by a number of variables. These macroscopic variables can, e.g., refer to the total volume, the positions of pistons in the system, etc. Then Ω will depend on the values of these variables. If a variable is not fixed, (e.g. we do not clamp a piston in a certain position), then because all the accessible states are equally likely in equilibrium, the free variable in equilibrium will be such that Ω is maximized as that is the most probable situation in equilibrium.
If the variable was initially fixed to some value then upon release and when the new equilibrium has been reached, the fact the variable will adjust itself so that Ω is maximized, implies that that the entropy will have increased or it will have stayed the same (if the value at which the variable was fixed happened to be the equilibrium value).
The entropy of a system that is not in equilibrium can be defined as:
Suppose we start from an equilibrium situation and we suddenly remove a constraint on a variable. Then right after we do this, there are a number Ω of accessible microstates, but equilibrium has not yet been reached, so the actual probabilities of the system being in some accessible state are not yet equal to the prior probability of 1 / Ω. We have already seen that in the final equilibrium state, the entropy will have increased or have stayed the same relative to the previous equilibrium state. Boltzmann's H-theorem, however, proves that the entropy will increase continuously as a function of time during the intermediate out of equilibrium state.
The generalized force, X, corresponding to the external variable x is defined such that Xdx is the work performed by the system if x is increased by an amount dx. E.g., if x is the volume, then X is the pressure. The generalized force for a system known to be in energy eigenstate Er is given by:
 energy eigenstates by counting how many of them have a value for
energy eigenstates by counting how many of them have a value for 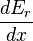 within a range between Y and Y + δY. Calling this number
within a range between Y and Y + δY. Calling this number  , we have:
, we have:
 will change because the energy eigenstates depend on x, causing energy eigenstates to move into or out of the range between E and E + δE. Let's focus again on the energy eigenstates for which
will change because the energy eigenstates depend on x, causing energy eigenstates to move into or out of the range between E and E + δE. Let's focus again on the energy eigenstates for which 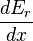 lies within the range between Y and Y + δY. Since these energy eigenstates increase in energy by Y dx, all such energy eigenstates that are in the interval ranging from E - Y dx to E move from below E to above E. There are
lies within the range between Y and Y + δY. Since these energy eigenstates increase in energy by Y dx, all such energy eigenstates that are in the interval ranging from E - Y dx to E move from below E to above E. There are
 , all these energy eigenstates will move into the range between E and E + δE and contribute to an increase in Ω. The number of energy eigenstates that move from below E + δE to above E + δE is, of course, given by
, all these energy eigenstates will move into the range between E and E + δE and contribute to an increase in Ω. The number of energy eigenstates that move from below E + δE to above E + δE is, of course, given by  . The difference
. The difference
 and
and  , therefore the above expression is also valid in that case.
, therefore the above expression is also valid in that case.
Expressing the above expression as a derivative w.r.t. E and summing over Y yields the expression:
One of the most famous responses to this question was suggested in 1929 by Leó Szilárd and later by Léon Brillouin. Szilárd pointed out that a real-life Maxwell's demon would need to have some means of measuring molecular speed, and that the act of acquiring information would require an expenditure of energy. But later exceptions were found.
One approach to handling Loschmidt's paradox is the fluctuation theorem, proved by Denis Evans and Debra Searles, which gives a numerical estimate of the probability that a system away from equilibrium will have a certain change in entropy over a certain amount of time. The theorem is proved with the exact time reversible dynamical equations of motion and the Axiom of Causality. The fluctuation theorem is proved utilizing the fact that dynamics is time reversible. Quantitative predictions of this theorem have been confirmed in laboratory experiments at the Australian National University conducted by Edith M. Sevick et al. using optical tweezers apparatus.
The paradox is averted by recognizing that the identity of the particles does not influence the entropy. In the conventional explanation, this is associated with an indistinguishability of the particles associated with quantum mechanics. However, a growing number of papers now take the perspective that it is merely the definition of entropy that is changed to ignore particle permutation (and thereby avert the paradox). The resulting equation for the entropy (of a classical ideal gas) is extensive, and is known as the Sackur-Tetrode equation.
The second law may be expressed in many specific ways, but the first formulation is credited to the German scientist Rudolf Clausius. The law is usually stated in physical terms of impossible processes. In classical thermodynamics, the second law is a basic postulate applicable to any system involving measurable heat transfer, while in statistical thermodynamics, the second law is a consequence of unitarity in quantum theory. In classical thermodynamics, the second law defines the concept of thermodynamic entropy, while in statistical mechanics entropy is defined from information theory, known as the Shannon entropy.
| Thermodynamics | ||||||||||

| ||||||||||
Contents |
Description
The first law of thermodynamics provides the basic definition of thermodynamic energy, also called internal energy, associated with all thermodynamic systems, but unknown in mechanics, and states the rule of conservation of energy in nature.However, the concept of energy in the first law does not account for the observation that natural processes have a preferred direction of progress. For example, spontaneously, heat always flows to regions of lower temperature, never to regions of higher temperature without external work being performed on the system. The first law is completely symmetrical with respect to the initial and final states of an evolving system. The key concept for the explanation of this phenomenon through the second law of thermodynamics is the definition of a new physical property, the entropy.
A change in the entropy (S) of a system is the infinitesimal transfer of heat (Q) to a closed system driving a reversible process, divided by the equilibrium temperature (T) of the system.[1]
Empirical temperature and its scale is usually defined on the principles of thermodynamics equilibrium by the zeroth law of thermodynamics.[2] However, based on the entropy, the second law permits a definition of the absolute, thermodynamic temperature, which has its null point at absolute zero.[3]
The second law of thermodynamics may be expressed in many specific ways,[4] the most prominent classical statements[3] being the original statement by Rudolph Clausius (1850), the formulation by Lord Kelvin (1851), and the definition in axiomatic thermodynamics by Constantin Carathéodory (1909). These statement cast the law in general physical terms citing the impossibility of certain processes. They have been shown to be equivalent.
Clausius statement
German scientist Rudolf Clausius is credited with the first formulation of the second law, now known as the Clausius statement:[4]- No process is possible whose sole result is the transfer of heat from a body of lower temperature to a body of higher temperature.[note 1]
Kelvin statement
Lord Kelvin expressed the second law in another form. The Kelvin statement expresses it as follows:[4]- No process is possible in which the sole result is the absorption of heat from a reservoir and its complete conversion into work.
Note that it is possible to convert heat completely into work, such as the isothermal expansion of ideal gas. However, such a process has an additional result. In the case of the isothermal expansion, the volume of the gas increases and never goes back without outside interference.
Principle of Carathéodory
Constantin Carathéodory formulated thermodynamics on a purely mathematical axiomatic foundation. His statement of the second law is known as the Principle of Carathéodory, which may be formulated as follows:[5]- In every neighborhood of any state S of an adiabatically isolated system there are states inaccessible from S.[6]
Equivalence of the statements
Suppose there is an engine violating the Kelvin statement: i.e.,one that drains heat and converts it completely into work in a cyclic fashion without any other result. Now pair it with a reversed Carnot engine as shown by the graph. The net and sole effect of this newly created engine consisting of the two engines mentioned is transferring heat from the cooler reservoir to the hotter one, which violates the Clausius statement. Thus the Clausius statement implies the Kelvin statement. We can prove in a similar manner that the Kelvin statement implies the Clausius statement, or, in a word, the two are equivalent.
from the cooler reservoir to the hotter one, which violates the Clausius statement. Thus the Clausius statement implies the Kelvin statement. We can prove in a similar manner that the Kelvin statement implies the Clausius statement, or, in a word, the two are equivalent.Corollaries
Perpetual motion of the second kind
Main article: perpetual motion
Prior to the establishment of the Second Law, many people who were interested in inventing a perpetual motion machine had tried to circumvent the restrictions of First Law of Thermodynamics by extracting the massive internal energy of the environment as the power of the machine. Such a machine is called a "perpetual motion machine of the second kind". The second law declared the impossibility of such machines.Carnot theorem
Carnot's theorem is a principle that limits the maximum efficiency for any possible engine. The efficiency solely depends on the temperature difference between the hot and cold thermal reservoirs. Carnot's theorem states:- All irreversible heat engines between two heat reservoirs are less efficient than a Carnot engine operating between the same reservoirs.
- All reversible heat engines between two heat reservoirs are equally efficient with a Carnot engine operating between the same reservoirs.
Clausius theorem
The Clausius theorem (1854) states that in a cyclic processThermodynamic temperature
Main article: Thermodynamic temperature
For an arbitrary heat engine, the efficiency is:Carnot's theorem states that all reversible engines operating between the same heat reservoirs are equally efficient. Thus, any reversible heat engine operating between temperatures T1 and T2 must have the same efficiency, that is to say, the effiency is the function of temperatures only:
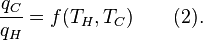
In addition, a reversible heat engine operating between temperatures T1 and T3 must have the same efficiency as one consisting of two cycles, one between T1 and another (intermediate) temperature T2, and the second between T2 andT3. This can only be the case if
Entropy
Main article: entropy (classical thermodynamics)
According to the Clausius equality, for a reversible process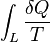 is path independent.
is path independent.So we can define a state function S called entropy, which satisfies
For any irreversible process, since entropy is a state function, we can always connect the initial and terminal status with an imaginary reversible process and integrating on that path to calculate the difference in entropy.
Now reverse the reversible process and combine it with the said irreversible process. Applying Clausius inequality on this loop,
Notice that if the process is an adiabatic process,then δQ = 0, so
 .
.Available useful work
See also: Available useful work (thermodynamics)
An important and revealing idealized special case is to consider applying the Second Law to the scenario of an isolated system (called the total system or universe), made up of two parts: a sub-system of interest, and the sub-system's surroundings. These surroundings are imagined to be so large that they can be considered as an unlimited heat reservoir at temperature TR and pressure PR — so that no matter how much heat is transferred to (or from) the sub-system, the temperature of the surroundings will remain TR; and no matter how much the volume of the sub-system expands (or contracts), the pressure of the surroundings will remain PR.Whatever changes to dS and dSR occur in the entropies of the sub-system and the surroundings individually, according to the Second Law the entropy Stot of the isolated total system must not decrease:
Now the heat leaving the reservoir and entering the sub-system is
It therefore follows that any net work δw done by the sub-system must obey
In sum, if a proper infinite-reservoir-like reference state is chosen as the system surroundings in the real world, then the Second Law predicts a decrease in X for an irreversible process and no change for a reversible process.
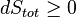 Is equivalent to
Is equivalent to 
This approach to the Second Law is widely utilized in engineering practice, environmental accounting, systems ecology, and other disciplines.
History
See also: History of entropy
The first theory of the conversion of heat into mechanical work is due to Nicolas Léonard Sadi Carnot in 1824. He was the first to realize correctly that the efficiency of this conversion depends on the difference of temperature between an engine and its environment.Recognizing the significance of James Prescott Joule's work on the conservation of energy, Rudolf Clausius was the first to formulate the second law during 1850, in this form: heat does not flow spontaneously from cold to hot bodies. While common knowledge now, this was contrary to the caloric theory of heat popular at the time, which considered heat as a fluid. From there he was able to infer the principle of Sadi Carnot and the definition of entropy (1865).
Established during the 19th century, the Kelvin-Planck statement of the Second Law says, "It is impossible for any device that operates on a cycle to receive heat from a single reservoir and produce a net amount of work." This was shown to be equivalent to the statement of Clausius.
The ergodic hypothesis is also important for the Boltzmann approach. It says that, over long periods of time, the time spent in some region of the phase space of microstates with the same energy is proportional to the volume of this region, i.e. that all accessible microstates are equally probable over a long period of time. Equivalently, it says that time average and average over the statistical ensemble are the same.
It has been shown that not only classical systems but also quantum mechanical ones tend to maximize their entropy over time. Thus the second law follows, given initial conditions with low entropy. More precisely, it has been shown that the local von Neumann entropy is at its maximum value with a very high probability.[9] The result is valid for a large class of isolated quantum systems (e.g. a gas in a container). While the full system is pure and therefore does not have any entropy, the entanglement between gas and container gives rise to an increase of the local entropy of the gas. This result is one of the most important achievements of quantum thermodynamics[dubious ].
Today, much effort in the field is attempting to understand why the initial conditions early in the universe were those of low entropy[10][11], as this is seen as the origin of the second law (see below).
Informal descriptions
The second law can be stated in various succinct ways, including:- It is impossible to produce work in the surroundings using a cyclic process connected to a single heat reservoir (Kelvin, 1851).
- It is impossible to carry out a cyclic process using an engine connected to two heat reservoirs that will have as its only effect the transfer of a quantity of heat from the low-temperature reservoir to the high-temperature reservoir (Clausius, 1854).
- If thermodynamic work is to be done at a finite rate, free energy must be expended.[12]
Mathematical descriptions
In 1856, the German physicist Rudolf Clausius stated what he called the "second fundamental theorem in the mechanical theory of heat" in the following form:[13]The entropy of the universe tends to a maximum.This statement is the best-known phrasing of the second law. Moreover, owing to the general broadness of the terminology used here, e.g. universe, as well as lack of specific conditions, e.g. open, closed, or isolated, to which this statement applies, many people take this simple statement to mean that the second law of thermodynamics applies virtually to every subject imaginable. This, of course, is not true; this statement is only a simplified version of a more complex description.
In terms of time variation, the mathematical statement of the second law for an isolated system undergoing an arbitrary transformation is:
- S is the entropy and
- t is time.
Derivation from statistical mechanics
In statistical mechanics, the Second Law is not a postulate, rather it is a consequence of the fundamental postulate, also known as the equal prior probability postulate, so long as one is clear that simple probability arguments are applied only to the future, while for the past there are auxiliary sources of information which tell us that it was low entropy. The first part of the second law, which states that the entropy of a thermally isolated system can only increase is a trivial consequence of the equal prior probability postulate, if we restrict the notion of the entropy to systems in thermal equilibrium. The entropy of an isolated system in thermal equilibrium containing an amount of energy of E is: is the number of quantum states in a small interval between E and E + δE. Here δE is a macroscopically small energy interval that is kept fixed. Strictly speaking this means that the entropy depends on the choice of δE. However, in the thermodynamic limit (i.e. in the limit of infinitely large system size), the specific entropy (entropy per unit volume or per unit mass) does not depend on δE.
is the number of quantum states in a small interval between E and E + δE. Here δE is a macroscopically small energy interval that is kept fixed. Strictly speaking this means that the entropy depends on the choice of δE. However, in the thermodynamic limit (i.e. in the limit of infinitely large system size), the specific entropy (entropy per unit volume or per unit mass) does not depend on δE.Suppose we have an isolated system whose macroscopic state is specified by a number of variables. These macroscopic variables can, e.g., refer to the total volume, the positions of pistons in the system, etc. Then Ω will depend on the values of these variables. If a variable is not fixed, (e.g. we do not clamp a piston in a certain position), then because all the accessible states are equally likely in equilibrium, the free variable in equilibrium will be such that Ω is maximized as that is the most probable situation in equilibrium.
If the variable was initially fixed to some value then upon release and when the new equilibrium has been reached, the fact the variable will adjust itself so that Ω is maximized, implies that that the entropy will have increased or it will have stayed the same (if the value at which the variable was fixed happened to be the equilibrium value).
The entropy of a system that is not in equilibrium can be defined as:
Suppose we start from an equilibrium situation and we suddenly remove a constraint on a variable. Then right after we do this, there are a number Ω of accessible microstates, but equilibrium has not yet been reached, so the actual probabilities of the system being in some accessible state are not yet equal to the prior probability of 1 / Ω. We have already seen that in the final equilibrium state, the entropy will have increased or have stayed the same relative to the previous equilibrium state. Boltzmann's H-theorem, however, proves that the entropy will increase continuously as a function of time during the intermediate out of equilibrium state.
Derivation of the entropy for reversible processes
The second part of the Second Law states that the entropy change of a system undergoing a reversible process is given by:The generalized force, X, corresponding to the external variable x is defined such that Xdx is the work performed by the system if x is increased by an amount dx. E.g., if x is the volume, then X is the pressure. The generalized force for a system known to be in energy eigenstate Er is given by:
 energy eigenstates by counting how many of them have a value for
energy eigenstates by counting how many of them have a value for 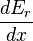 within a range between Y and Y + δY. Calling this number
within a range between Y and Y + δY. Calling this number  , we have:
, we have: will change because the energy eigenstates depend on x, causing energy eigenstates to move into or out of the range between E and E + δE. Let's focus again on the energy eigenstates for which
will change because the energy eigenstates depend on x, causing energy eigenstates to move into or out of the range between E and E + δE. Let's focus again on the energy eigenstates for which 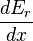 lies within the range between Y and Y + δY. Since these energy eigenstates increase in energy by Y dx, all such energy eigenstates that are in the interval ranging from E - Y dx to E move from below E to above E. There are
lies within the range between Y and Y + δY. Since these energy eigenstates increase in energy by Y dx, all such energy eigenstates that are in the interval ranging from E - Y dx to E move from below E to above E. There are , all these energy eigenstates will move into the range between E and E + δE and contribute to an increase in Ω. The number of energy eigenstates that move from below E + δE to above E + δE is, of course, given by
, all these energy eigenstates will move into the range between E and E + δE and contribute to an increase in Ω. The number of energy eigenstates that move from below E + δE to above E + δE is, of course, given by  . The difference
. The difference and
and  , therefore the above expression is also valid in that case.
, therefore the above expression is also valid in that case.Expressing the above expression as a derivative w.r.t. E and summing over Y yields the expression:
Derivation for systems described by the canonical ensemble
If a system is in thermal contact with a heat bath at some temperature T then, in equilibrium, the probability distribution over the energy eigenvalues are given by the canonical ensemble:General derivation from unitarity of quantum mechanics
The time development operator in quantum theory is unitary, because the Hamiltonian is hermitian. Consequently the transition probability matrix is doubly stochastic, which implies the Second Law of Thermodynamics.[14][15] This derivation is quite general, based on the Shannon entropy, and does not require any assumptions beyond unitarity, which is universally accepted. It is a consequence of the irreversibility or singular nature of the general transition matrix.Non-equilibrium states
Statistically it is possible for a system to achieve moments of non-equilibrium. In such statistically unlikely events where hot particles "steal" the energy of cold particles enough that the cold side gets colder and the hot side gets hotter, for an instant. Such events have been observed at a small enough scale where the likelihood of such a thing happening is significant.[16] The physics involved in such an event is described by the fluctuation theorem.Controversies
Maxwell's demon
Main article: Maxwell's demon
Maxwell imagined one container divided into two parts, A and B. Both parts are filled with the same gas at equal temperatures and placed next to each other. Observing the molecules on both sides, an imaginary demon guards a trapdoor between the two parts. When a faster-than-average molecule from A flies towards the trapdoor, the demon opens it, and the molecule will fly from A to B. The average speed of the molecules in B will have increased while in A they will have slowed down on average. Since average molecular speed corresponds to temperature, the temperature decreases in A and increases in B, contrary to the second law of thermodynamics.One of the most famous responses to this question was suggested in 1929 by Leó Szilárd and later by Léon Brillouin. Szilárd pointed out that a real-life Maxwell's demon would need to have some means of measuring molecular speed, and that the act of acquiring information would require an expenditure of energy. But later exceptions were found.
Loschmidt's paradox
Loschmidt's paradox, also known as the reversibility paradox, is the objection that it should not be possible to deduce an irreversible process from time-symmetric dynamics. This puts the time reversal symmetry of (almost) all known low-level fundamental physical processes at odds with any attempt to infer from them the second law of thermodynamics which describes the behavior of macroscopic systems. Both of these are well-accepted principles in physics, with sound observational and theoretical support, yet they seem to be in conflict; hence the paradox.One approach to handling Loschmidt's paradox is the fluctuation theorem, proved by Denis Evans and Debra Searles, which gives a numerical estimate of the probability that a system away from equilibrium will have a certain change in entropy over a certain amount of time. The theorem is proved with the exact time reversible dynamical equations of motion and the Axiom of Causality. The fluctuation theorem is proved utilizing the fact that dynamics is time reversible. Quantitative predictions of this theorem have been confirmed in laboratory experiments at the Australian National University conducted by Edith M. Sevick et al. using optical tweezers apparatus.
Gibbs paradox
Main article: Gibbs paradox
In statistical mechanics, a simple derivation of the entropy of an ideal gas based on the Boltzmann distribution yields an expression for the entropy which is not extensive (is not proportional to the amount of gas in question). This leads to an apparent paradox known as the Gibbs paradox, allowing, for instance, the entropy of closed systems to decrease, violating the second law of thermodynamics.The paradox is averted by recognizing that the identity of the particles does not influence the entropy. In the conventional explanation, this is associated with an indistinguishability of the particles associated with quantum mechanics. However, a growing number of papers now take the perspective that it is merely the definition of entropy that is changed to ignore particle permutation (and thereby avert the paradox). The resulting equation for the entropy (of a classical ideal gas) is extensive, and is known as the Sackur-Tetrode equation.
Poincaré recurrence theorem
The Poincaré recurrence theorem states that certain systems will, after a sufficiently long time, return to a state very close to the initial state. The Poincaré recurrence time is the length of time elapsed until the recurrence. The result applies to physical systems in which energy is conserved. The Recurrence theorem apparently contradicts the Second law of thermodynamics, which says that large dynamical systems evolve irreversibly towards the state with higher entropy, so that if one starts with a low-entropy state, the system will never return to it. There are many possible ways to resolve this paradox, but none of them is universally accepted[citation needed]. The most typical argument is that for thermodynamical systems like an ideal gas in a box, recurrence time is so large that for all practical purposes it is infinite.Heat death of the universe
Main article: Heat death of the universe
According to the second law the entropy of any isolated system, such as the entire universe, never decreases. If the entropy of the universe has a maximum upper bound then when this bound is reached the universe has no thermodynamic free energy to sustain motion or life, that is, the heat death is reached.



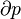
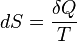



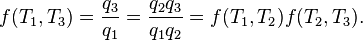
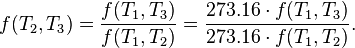






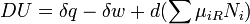





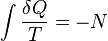
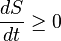
![S = k \log\left[\Omega\left(E\right)\right]\,](http://upload.wikimedia.org/math/c/0/4/c04285070a2bf9a8397a5d9e90b6076c.png)
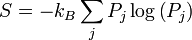

![\frac{1}{k T}\equiv\beta\equiv\frac{d\log\left[\Omega\left(E\right)\right]}{dE}](http://upload.wikimedia.org/math/5/4/3/5436a8cd068ae0b6c79db1cf67cf3550.png)











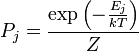

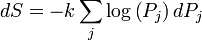

No comments:
Post a Comment